Since higher-abstraction languages like Julia and Python naturally reside closer to algorithmic thinking, you don’t have to worry about — or get caught up in — implementation details. Consequently, these languages are better for exploration and prototyping than lower-abstraction languages like C or Java. Indeed, if the system allows, implementing the designed system in the higher-abstraction language may be better because those languages are more adaptable for implementing domain-specific language, simplifying validation of the algorithm implementation and maintenance.
But what does prototyping and exploration in a higher-abstraction language look like in practice? In this blog post, we use Julia to walk through a prototyping and exploration exercise.
Contents
Programmatically Decoding Morse Code Message from UCSD Tower
Say we came across this tower with a signal lamp fixed atop while walking around the University of California, San Diego:
The tower obviously seems like it is transmitting a message. And that message is most likely Morse code. How would we decode it programmatically? In the most general terms, we want to implement this block diagram:
We want to take the video as input and extract the message. But where do we start?
Step 1: Simplify the Challenge

The first thing we do is simplify the problem. By converting the color video to grayscale, we reduce the problem set from three luminance values (red, green and blue) to one. We can also crop down to the video portion with the highest signal-to-noise ratio (indicated by the red box), which can be done offline using a tool like FFmpeg.
Step 2: Engage with Julia
Once that is done, we can load the video into Julia because libraries for reading video and converting it into native vectors exist. As part of the prototyping effort, we don’t have to worry about converting compressed video into a usable format. Julia also has a REPL, so we don’t have to construct a program to try things out. We can just play interactively from the Julia prompt.
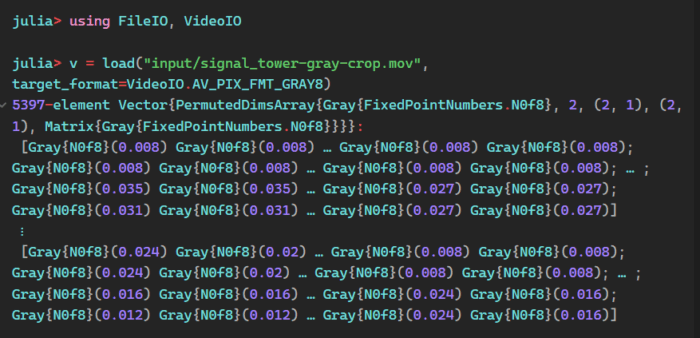
Step 3: Extract Luminance Values
With the video loaded into Julia, we want to simplify the problem even more. Since we’re looking at bright, blinking lights, taking the maximum luminance value of each frame seems reasonable. When the light is on, it will be the brightest value. When the light is off, the background value will prevail. Developers can easily take the luminance value in Julia because advanced vector manipulations are baked into the language.
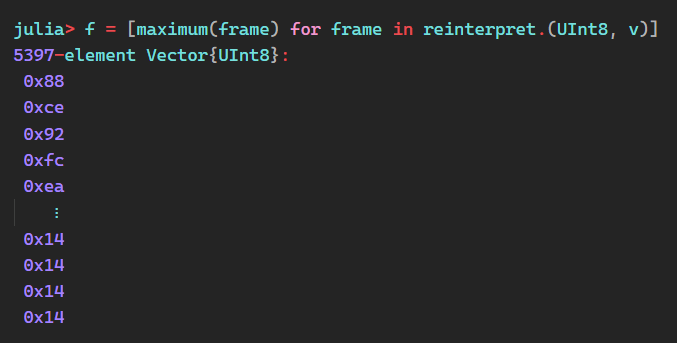
In block diagram terms, we have transformed the video into a time series of integers.
Step 4: Explore the Data
Examining the data — which we can do because a plotting package is available in Julia — we verify that good separation between video frames exists with the signal lamp on and with the signal lamp off.

Zooming in confirms this.

Step 5: Map Luminance to On/Off
This separation means we can transform the maximum luminance values into an on-off signal using a simple threshold function. The block diagram looks like this:
In Julia, this translates into a simple elementwise comparison.
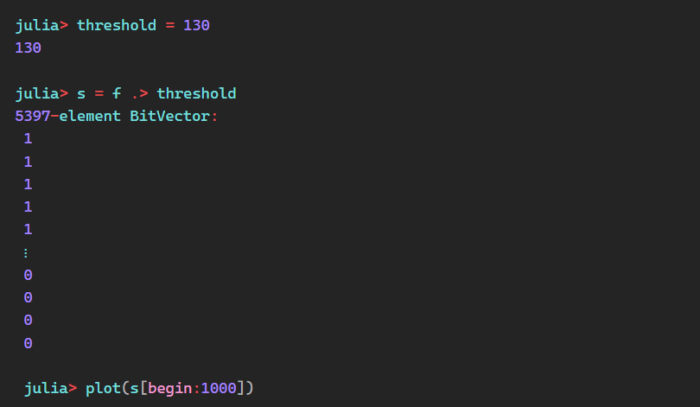
This comparison looks very promising!
Morse code consists of symbols (dots and dashes) and separators (symbol separators, letter separators and word separators), each defined by the duration — or length — of a run of highs for symbols or lows for separators.
The base unit in Morse code is the length of a dot, defined as one time unit. A dash is three time units long. A symbol separator is one time unit long. A letter separator is three time units long. And a word separator is seven time units long. Looking at the signal plot, we can see all of these elements.
Step 6: Detect Edges and Their Indices
The next step is determining the length of the runs. To compute those, we need to know whether an edge rises or falls and the frame indices of the transition edges in the signal.
Edges are found using the equation e(t) = s(t+1) – s(t). When e(t) is 1, that indicates a rising edge, whereas e(t) is -1 points to a falling edge. The signal runs are indicated when e(t) is 0. Edge indices are the values of t where e(t) is not 0.
Julia leverages simple vector arithmetic to find edges. You can find the edge indices using the built-in function findall.
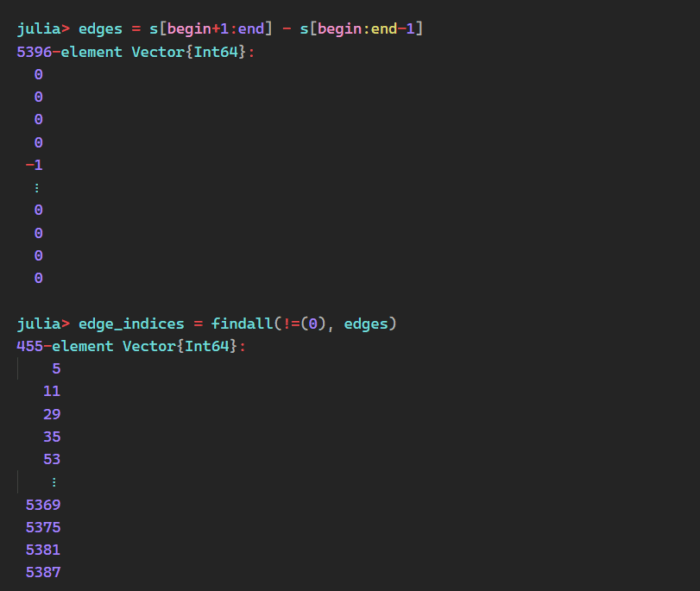
Step 7: Confirm Element Consistency
We have the run lengths, but do they cluster into our expected groups of dots, dashes and multiple separators? To verify the element spacing, we need to convert the edges and edge indices into high and low run lengths by writing our first function in Julia:
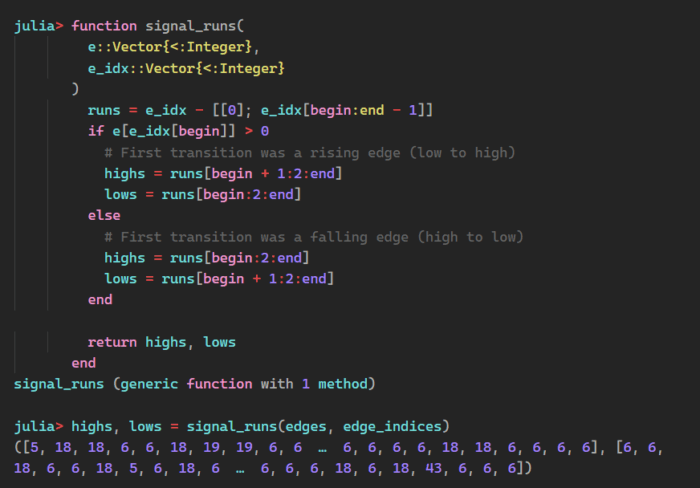
Step 8: Create Histograms for Better Understanding
With the high and low runs computed, we can plot their histograms.


A dot is six frames (one time unit), a dash is 18 frames (three time units), a symbol separator is six frames (one time unit), a letter separator is 18 frames (three time units) and a word separator is 42 frames (seven time units) — just as expected.
Step 9: Decode the Message
Based on that information, we can now choose threshold values to differentiate dots and dashes (and also symbol and letter separators) and letter and word separators. With that, we have enough information to decode our message.
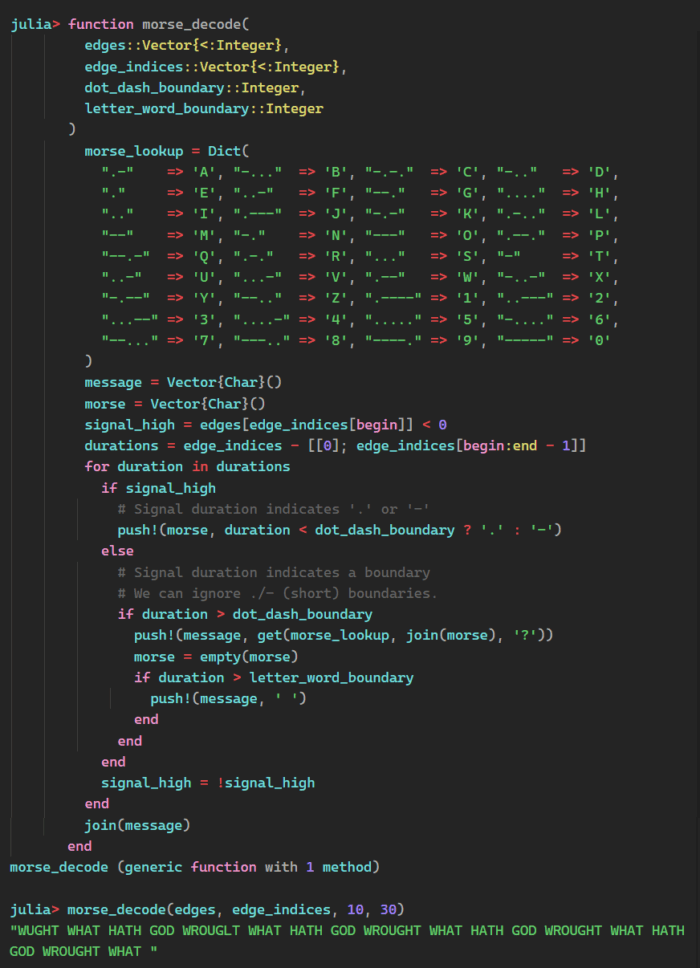
“WHAT HATH GOD WROUGHT” was the first public telegraphic message ever sent. Samuel Morse transmitted it from the U.S. Capitol in Washington, D.C., to his assistant, Alfred Vail, in a Baltimore train station on May 24, 1844.
We can decode the crop video, but what about the full-frame video?
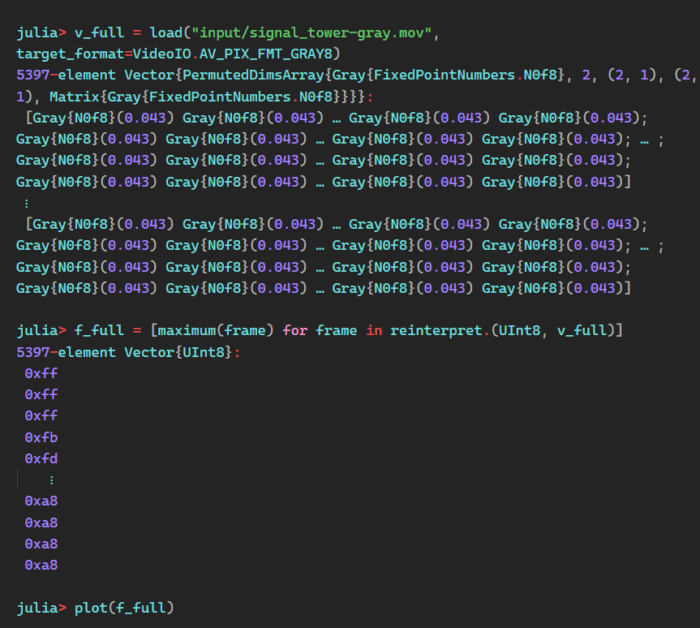
The highs look the same, but there’s quite a bit more noise on the lows. If we adjust the threshold up, we should still be able to decode the message.
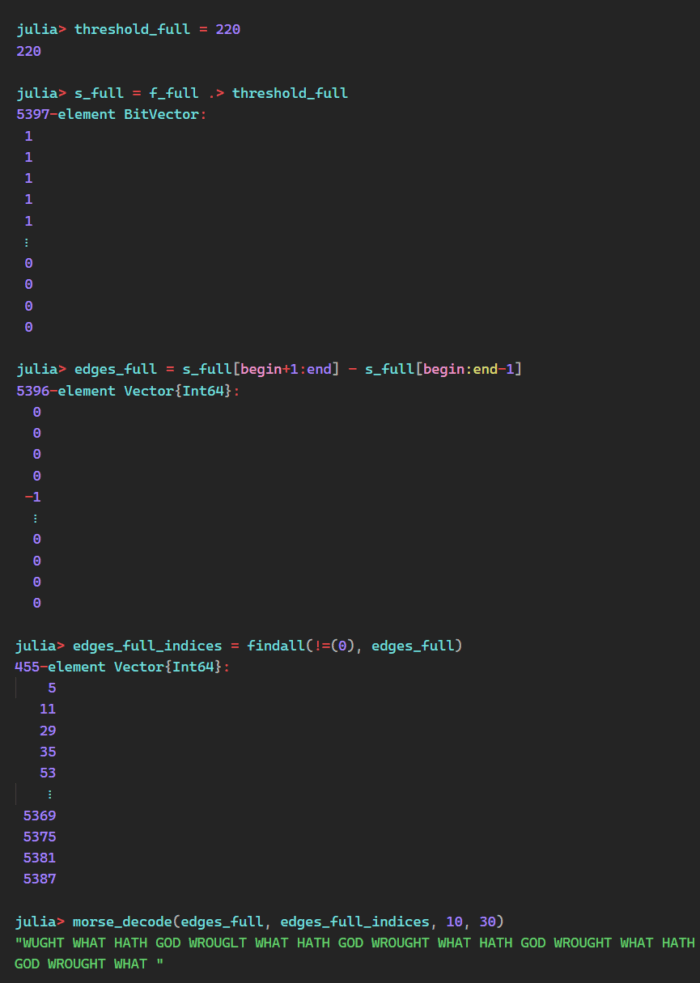
Indeed, we can. The problem: We have to manually choose the threshold and boundary values each time we want to decode a message. Ideally, this would be automated, which we set out to do at the beginning.
Step 10: Automate the Process with an Automatic Threshold Detector
Looking at the distributions of f for the crop and full-frame video and considering how we chose the threshold, we can develop an automatic threshold detector.


To determine the threshold, we estimate the midpoint between the means of the two clusters. This estimation can be calculated iteratively by guessing an initial threshold (say, halfway between the minimum and maximum), grouping the signals into two bins (below and above the threshold), calculating the mean of those bins, recomputing the threshold and repeating until the threshold doesn’t move (much).
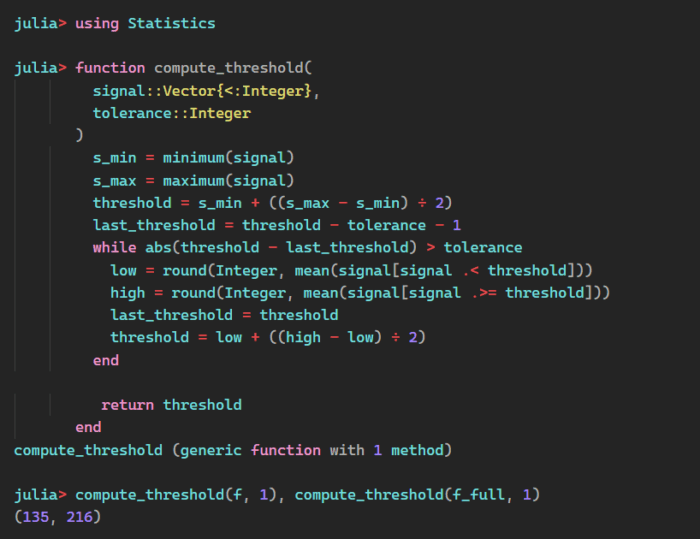
We eyeballed 130 and 220 for the thresholds, so the algorithm seems reasonable.
This brings it all together.
Take the incoming video and find the brightest pixel in each frame, f(t). Use those values to calculate a threshold value and convert the pixel stream into a signal, s(t). Convert s(t) into edges and edge indices and transform those into runs of lows and highs. Use the runs to determine the dot-dash boundary and the letter-space boundary. Finally, decode the message using the edges, edge indices and boundaries.
The code looks like this:
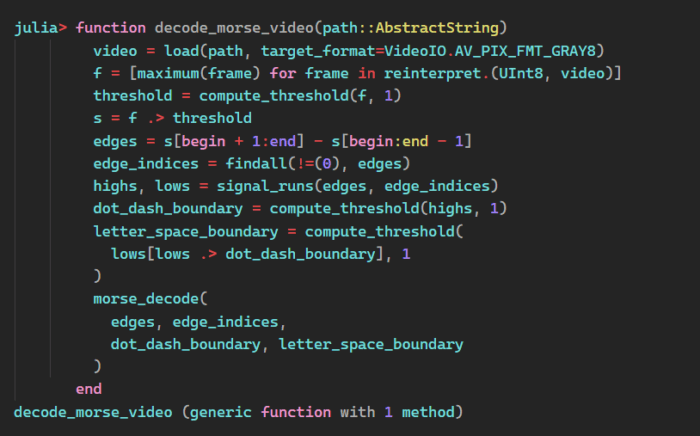
And it works on both the crop and full-frame videos.

From Prototype to Solution: Speedy Algorithm Development
We have successfully created a function that takes a path to a video as input and outputs the embedded Morse code message.
Using Julia for exploration and prototyping, we quickly developed — and implemented — an algorithm for decoding Morse code from video. The resulting code is very readable. Given sufficient compute resources and system constraints, a derivative from the prototype code could be used in production, making implementation easy to maintain. Even if translation to another language is required, a prototype in a higher-abstraction language can be used as a source of truth to compare a production implementation against and an impetus for foundational abstraction implementations in whatever the production language may be.
