The world is moving in the direction of HDTV, but NTSC “standard def” signals are still common for many reasons and will remain so. One important reason is that cameras that output NTSC are widely available and cheap! Many applications, including a lot of security applications, simply don’t require the resolution of HDTV — and don’t want to incur the camera cost and bandwidth hit it requires.
So, what is resolution anyway, especially with regards to an analog NTSC video signal? Analog video cameras, especially in the CCTV industry, are sold using “horizontal TV lines”, or HTVL, as one of their key specifications. Unfortunately, the math behind that concept is not well understood.
To understand resolution we start with the aspect ratio. The aspect ratio of a picture is the ratio of its width to its height. Different aspect ratios are in use today for different applications. HDTV has an aspect ratio of 16:9. Standard definition TV has an aspect ratio of 4:3. In general, resolution is measured in a circle whose diameter is equivalent to a picture’s smallest dimension. The diagram below illustrates the case for NTSC:
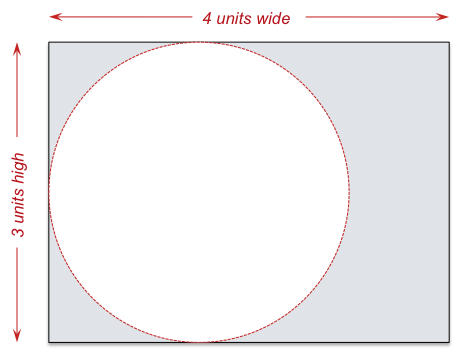
In the above diagram, the circle has a diameter of 3 units or 1 “picture height.”
Now, imagine a uniformly spaced sequence of vertical black lines of constant width. The white space between the black lines should be the same width as the black lines themselves. Counting both black and white lines, how many lines can be physically resolved within the above circle? The answer to this question is the horizontal resolution. Before we can go further, we need some facts regarding NTSC:
First, there are 525 scan lines per picture, and the horizontal scanning frequency is
f_{h}=\dfrac{13,500,000}{858}=15,734.26573
This is one of NTSC’s magic numbers. The horizontal line time is therefore approximately 1 / 15,734.26573, or 63.5556 ?sec.
Second, the horizontal blanking period is 10.7 ?sec. During this period, a horizontal sync pulse is transmitted, as well as a chroma burst (to enable decoders to demodulate the correct color), and a reference black level. The active line time the period during which information is actually being drawn on the visible screen — is therefore 63.5556 ? 10.7, or 52.8556 ?sec.
Finally, the highest broadcast luminance signal is 4.2 MHz.
Based on the above, we can compute the highest horizontal resolution that can be present in an NTSC signal as follows:
R_{H}=2(4.2)(52.8556)\Big(\dfrac{3}{4}\Big)=333 \space lines
The product of the middle two parameters is the number of complete cycles present in one active line (the MHz and microseconds cancel); the factor of 2 is present because we count both the white and black lines in the horizontal resolution calculation. Multiplying by three-fourths takes into account the circle in which the horizontal resolution is defined. Bear in mind that this pattern would be displayed on an NTSC TV as grey, not as a crisp sequence of black and white lines, due to the rolloff of the various filters used to limit the video bandwidth.
In the vertical direction, resolution is limited by the number of scan lines. There are 480 scan lines in the visible area of a picture, so one would be tempted to assert that the vertical resolution is 480. However, imagine a uniformly spaced sequence of horizontal lines analogous to the vertical line pattern described above. We want this horizontal pattern to be discernible regardless of its relative relationship to the scanning lines. In other words, as the pattern is displaced vertically, the number of lines should still be easily resolved.
Imagine that we have a pattern of 480 horizontal lines, alternating black and white. When these lines are exactly midway between the scanning lines, the resulting picture will be grey. Why? Because the scanning will average the black and white inputs together for each reproduced line. So a pattern of 480 lines would not be discernible: the resolution must be less. The Kell factor measures by how much the vertical resolution is reduced relative to the number of scan lines, and it is usually assumed to be around 0.7 for a stationary pattern. This implies the following vertical resolution:
R_{v}=0.7(480)=336 \space lines
The horizontal and vertical resolutions are therefore approximately equal. This was one of the design goals of NTSC.
Note that the Kell factor is sometimes assumed to be a larger number for a pattern in motion because visual averaging will cause the eye to “ignore” the occasional grey or blurry pattern. Values as high as 0.9 are assumed for moving images.
Note further that the reason the Kell factor does not apply horizontally is that it is possible to put down the dots on a CRT so close that regardless of the horizontal phase of a 4.2 Mhz vertical line pattern, it will be resolved. However, the Kell factor does apply in the horizontal direction for a digital display such as a computer monitor or LCD panel.
In a digital SDTV system based on the CCIR 601 digital sampling standard, the luminance information is sampled at 13.5 Mhz. The number of samples per active line is therefore given by 13.5 x 52.8556 = 713.56. This number is often rounded up to 720 samples; rounding up provides some headroom on either side of the visible line to hide the edge effects of various digital processing operations such as filtering. Plus, margin is generally good in any design!
Nyquist sampling theory says that sampling at 13.5 Mhz would theoretically allow a horizontal frequency as high as 13.5 / 2 = 6.75 Mhz to be captured. However, because of the inability to implement perfect anti-aliasing filters, this cannot be achieved in practice. A reduction factor of 0.75 is appropriate, implying that the CCIR-601 sampling standard is good for horizontal frequencies as high as 0.75 x 6.75 = 5.06 Mhz. This is substantially better than old-fashioned analog NTSC broadcasts. Therefore, on a good monitor with analog component input, a CCIR-601 signal can achieve the following horizontal resolution:
R_{H,601}=2(5.06)(52.8556)(0.75)=401 \space lines
For a SIF resolution picture (360×240), we are effectively sampling at 6.75 Mhz, not 13.5 Mhz, so the highest horizontal frequency that can be reproduced is 0.75 x (6.75/2) = 2.53 Mhz, which corresponds to a horizontal resolution of:
R_{H,SIF}=2(2.53)(52.8556)(0.75)=200 \space lines
Bear in mind that to achieve this number one needs to do an excellent job of filtering. In the case of displaying a SIF picture on a computer monitor, we can approximate the horizontal resolution by using a Kell factor in the horizontal direction. This yields the following:
R_{H,SIF,Kell}=360(0.7)(0.75)=189 \space lines
In the above, the 0.7 is the Kell factor and the 0.75 is to account for the aspect ratio (remember, resolution is computed inside the circle). A value of 360 was used for purity’s sake. The MPEG world uses 352 and 704 because they are related by a factor of 2 and both are multiples of 16 (360 is not a multiple of 16). It also means there is a little less data to compress!
Mike Perkins, Ph.D., is a managing partner of Cardinal Peak and an expert in algorithm development for video and signal processing applications.
